Regional Convergence, Spatial Scale, and Spatial Dependence:

Evidence from Homicides and Personal Injuries in Colombia 2010-2018

Felipe Santos-Marquez
Master’s student
Graduate School of International Development
Nagoya University, JAPAN

Carlos Mendez
Graduate School of International Development
Nagoya University, JAPAN

Prepared for the 2020 Bolivian Conference on Development Economics July 27th

[ Working paper available at: https://felipe-santos.rbind.io/]

1 / 20

Motivation:

Beyond GDP, socio-economic variables and their convergence are relevant for development studies (Royuela et al 2015)
Persistent income differences, differences in health indicators and in "general" regional inequality in Colombia.
Scarce academic literature on convergence at the municipal level.

Research Objective:

Study convergence/divergence of homicide rates (NMR) and personal injury rates (NPIR) across municipalities and departments in Colombia over 2010-2018.
Analyze spatial autocorrelation and its robustness at different disaggregation levels.

Methods:

Classical convergence framework (Barro and Sala-i-Martin 1992)
Distributional convergence framework (Quah 1996; Hyndman et. al 1996)
Spatial convergence (spatial lag and spatial error models)
Spatial autocorrelation (Moran's I and differential Moran's I)

2 / 20

Main Results:

Sigma Convergence for both homicide and personal injury rates at the state level, Beta Convergence for both levels and rates.
Clustering dynamics
- NMR State level: 4+? convergence clusters
- NMR Municipal level: 2+? convergence clusters
- NPIR State level: 2 convergence clubs
- NPIR Municipal level: stagnation and 2 convergence clubs
Spatial Autocorrelation robust only at the municipality level

3 / 20

Outline of this presentation

Data description Non crime rates
Global convergence: Using classical summary measures
- Beta convergence
- Sigma convergence
Regional disaggregation:
- Distribution dynamics framework
- Distributional convergence
Global spatial autocorrelation:
- Disaggreagation effects
Policy discussion
- The Colombian National Development Plan 2018-22
Concluding Remarks

4 / 20

(1) Data:

Total number of homicides and personal injuries in Colombia per year from 2010 until 2018 (data taken from the national police).
Data is agreggated at the municipal and departmental levels.
Population census and estimates for states and municipalities (data from the National Bureau of Statistics).
Raw rates computed $$raw\space rates = crimes / population$$
Non crime rates computed　 $$NCR= 10000- raw\ rate * 10000$$
Survival rates are chosen because positively defined variables are a standard in the convergence literature.

5 / 20

Non-crime variables over time

6 / 20

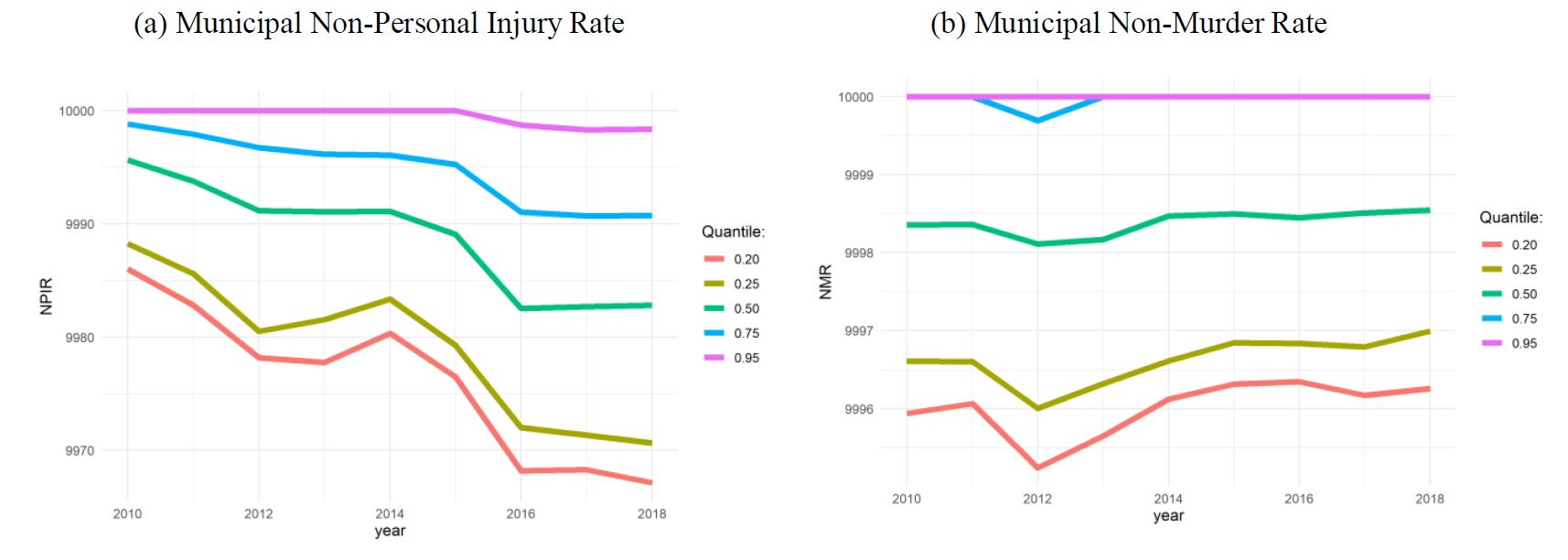
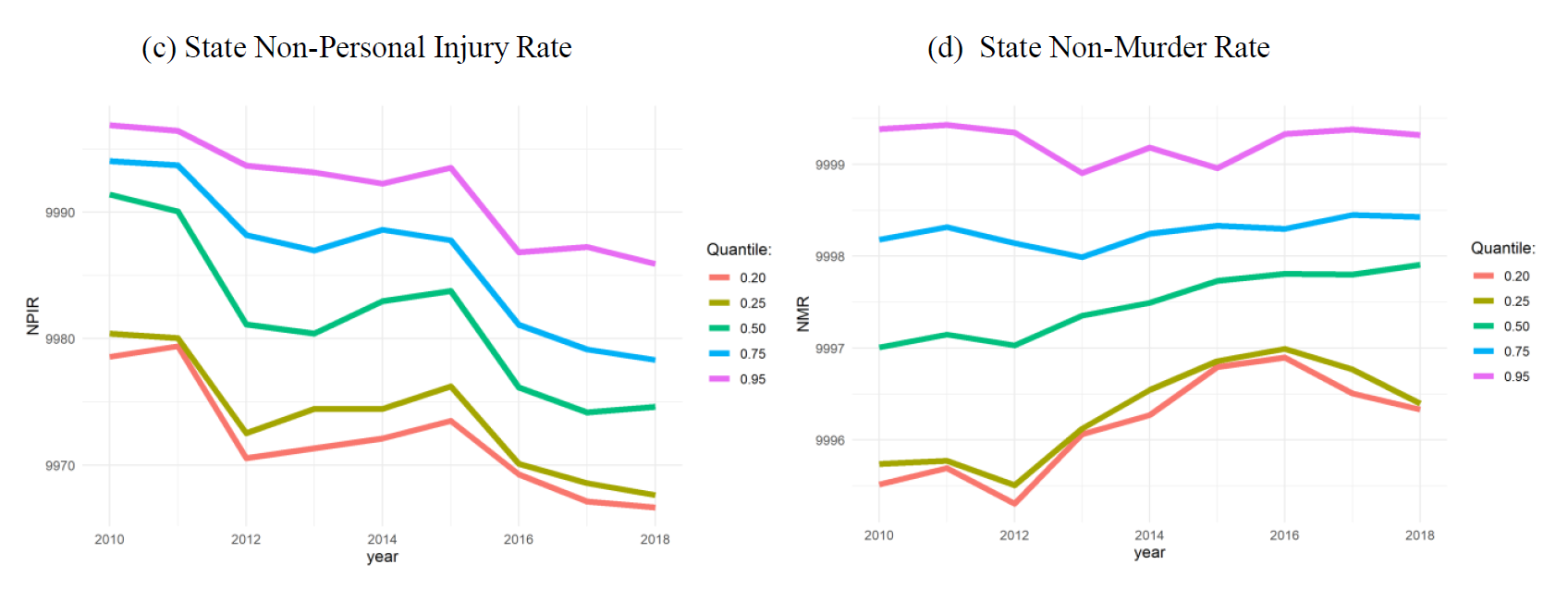
(2) Global convergence:

Beta convergence (catch-up process) $log{\frac{Y_{iT}}{Y_{i0}}}=\alpha +\beta \cdot log(Y_{i0})+ \epsilon$

Spatial Beta models

Spatial lag Model:　　　 $\log \frac{Y_{i T}}{Y_{i 0}}=\alpha+\beta \cdot \log \left(Y_{i 0}\right)+\rho W \log \frac{Y_{i T}}{Y_{i 0}}+\varepsilon_{t}$

Spatial Error Model: 　　　　　 $\log \frac{Y_{i T}}{Y_{i 0}}=\alpha+\beta \cdot \log \left(Y_{i 0}\right)+\lambda W \varepsilon_{t}+u_{t}$

Sigma convergence (the dispersion of the data decreases over time)

7 / 20

Classical Convergence results (NMR)

States- Sigma and Beta convergence

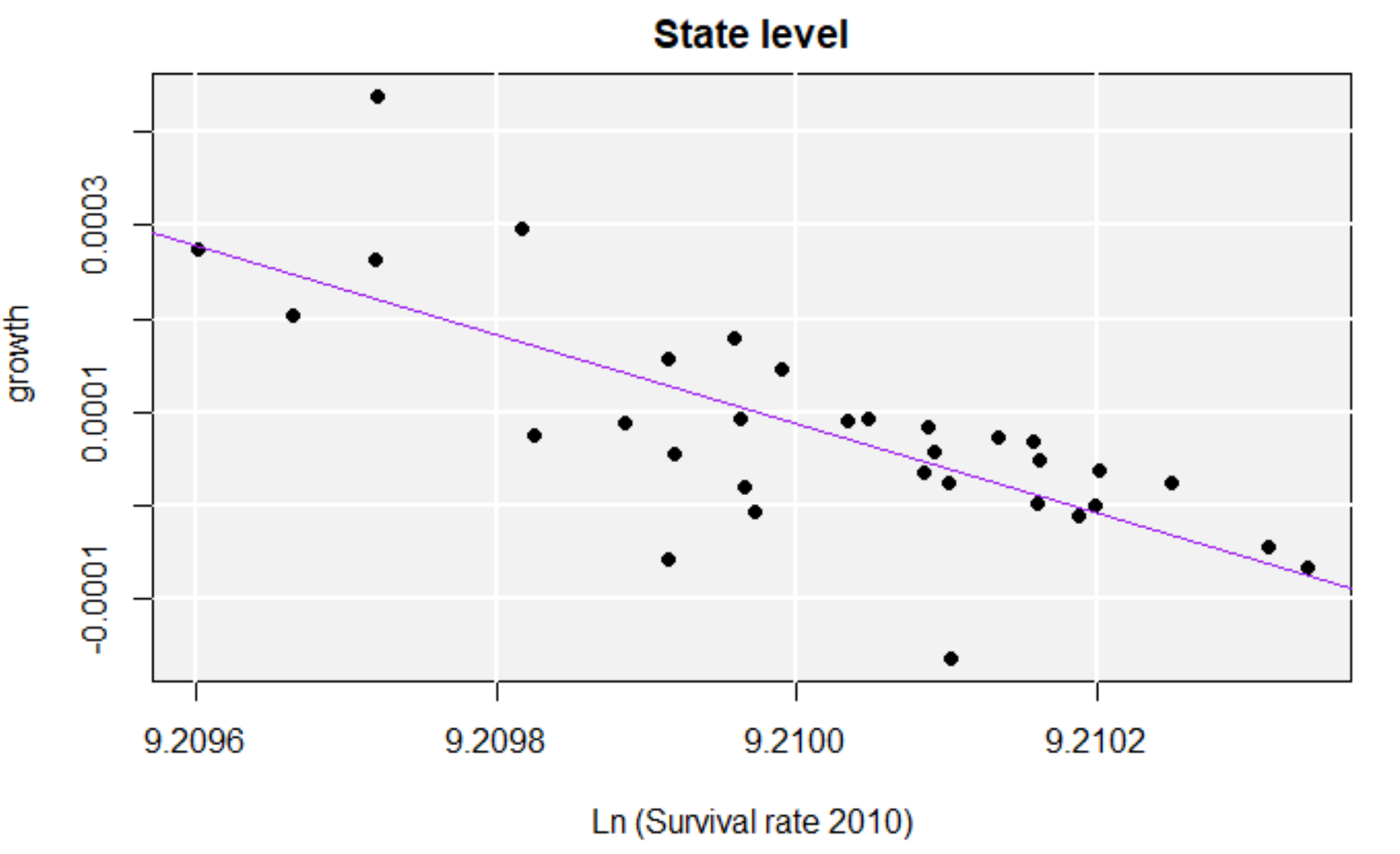
Municipalities - ONLY Beta convergence

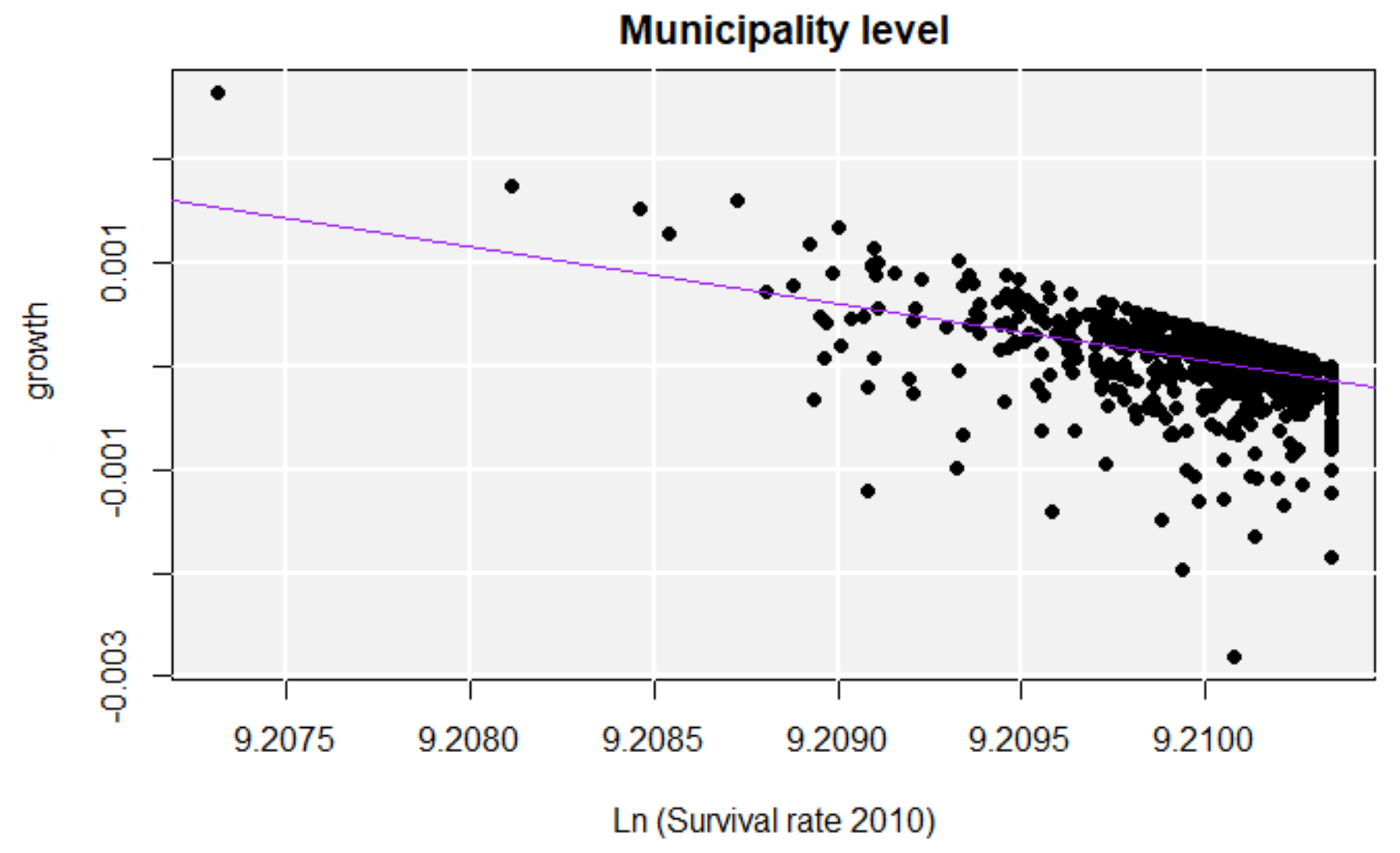
Sigma convergence results

8 / 20

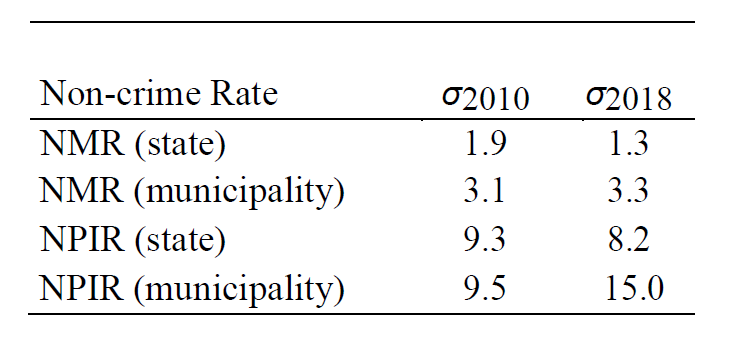
Beta and sigma convergence summary

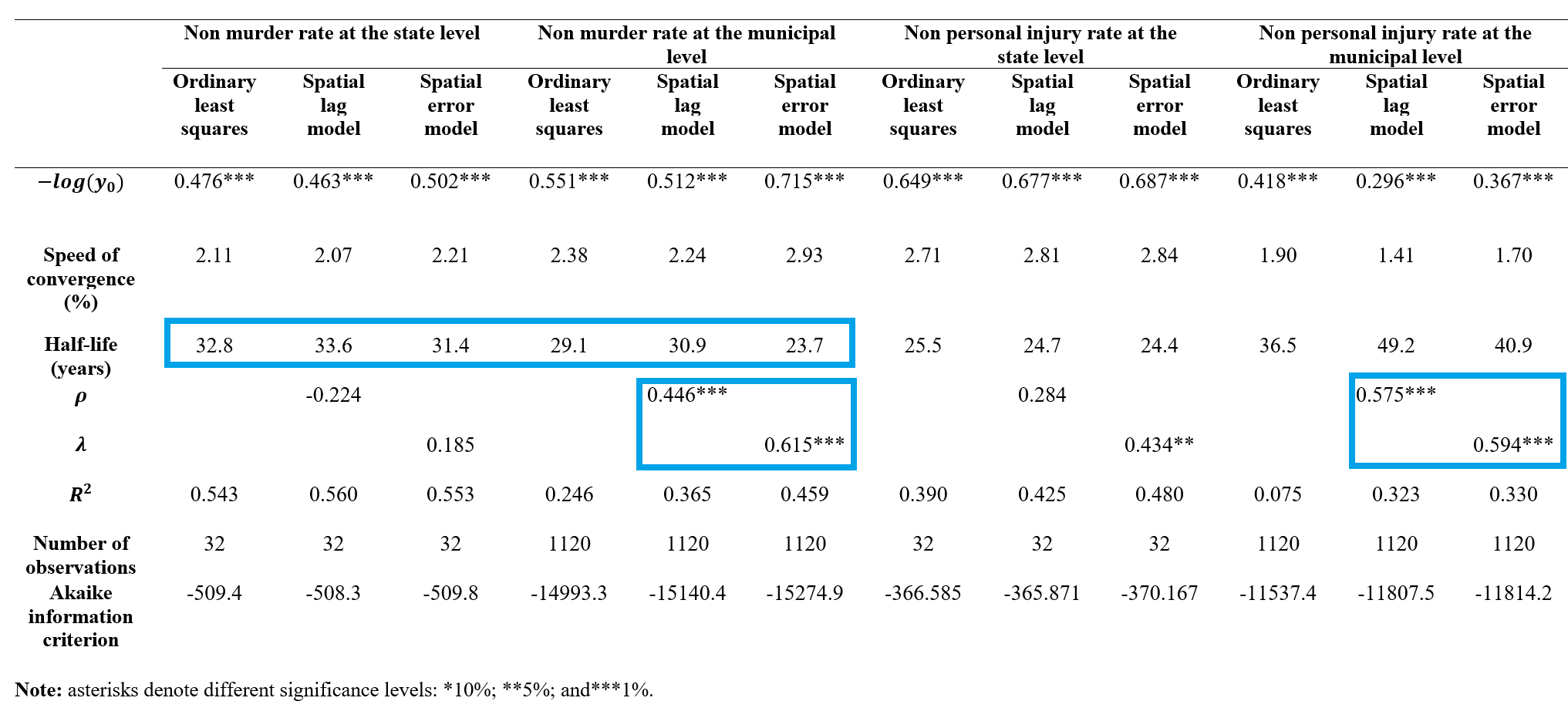
Lagrange multiplier tests also indicate that the SEM is the best fitting model.
Royuela and García (2015) also reported that the $\rho$ and $\lambda$ coefficients were NOT significant at the state level over the period 1990 to 2005.
The authors reported half-lives of 15.3, 11.5 and 15.8 years.

9 / 20

(3) State and Municipality disaggregation:

The distribution dynamics framework

10 / 20

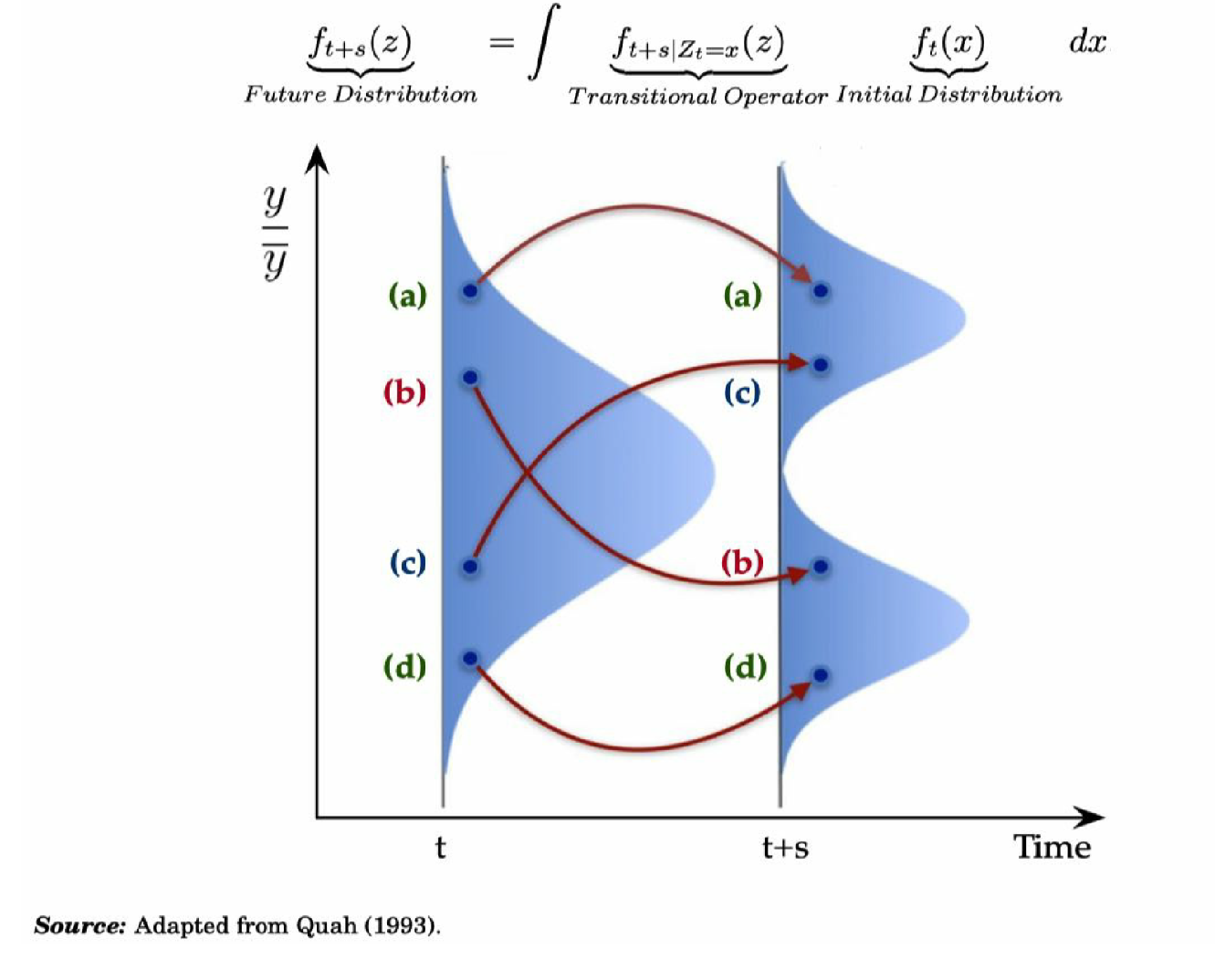
The distribution dynamics framework

Convergence, divergence and stagnation

11 / 20

(3) Local convergence clusters

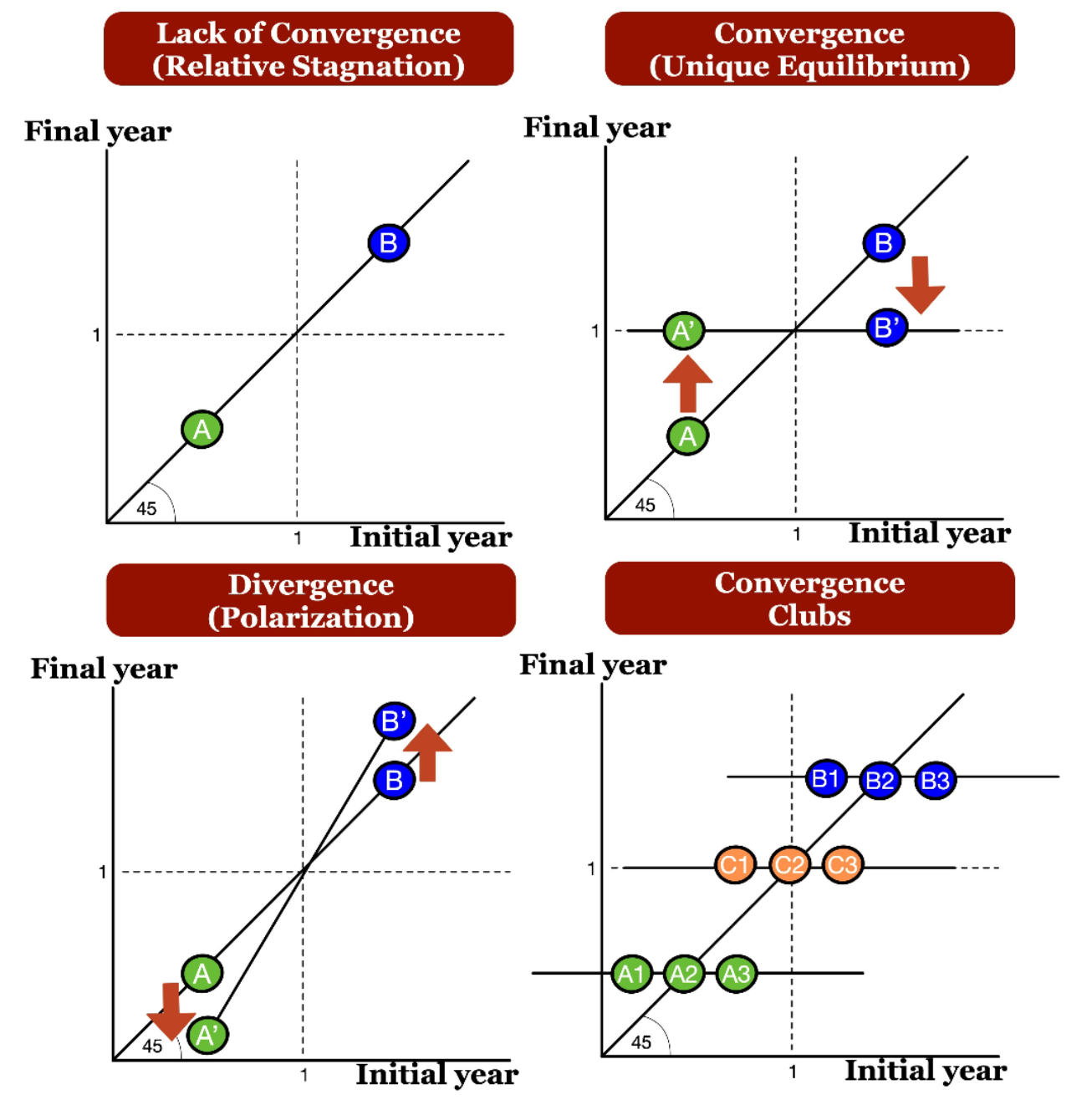
NMR State level: 4+? convergence clusters

NMR Municipal level: 2+? convergence clusters

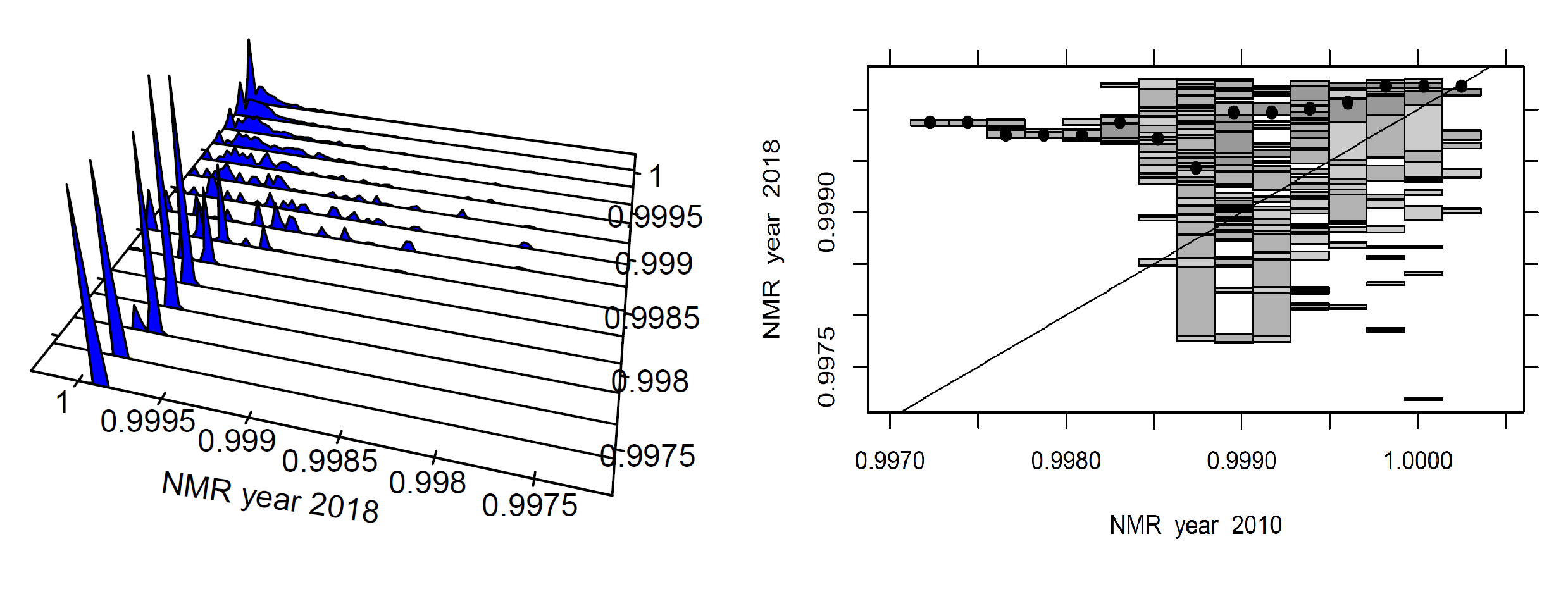
NPIR State level : 2 convergence clubs

NPIR Municipal level : stagnation and 2 convergence clubs

12 / 20

NMR at both levels

State level: 4+? convergence clusters

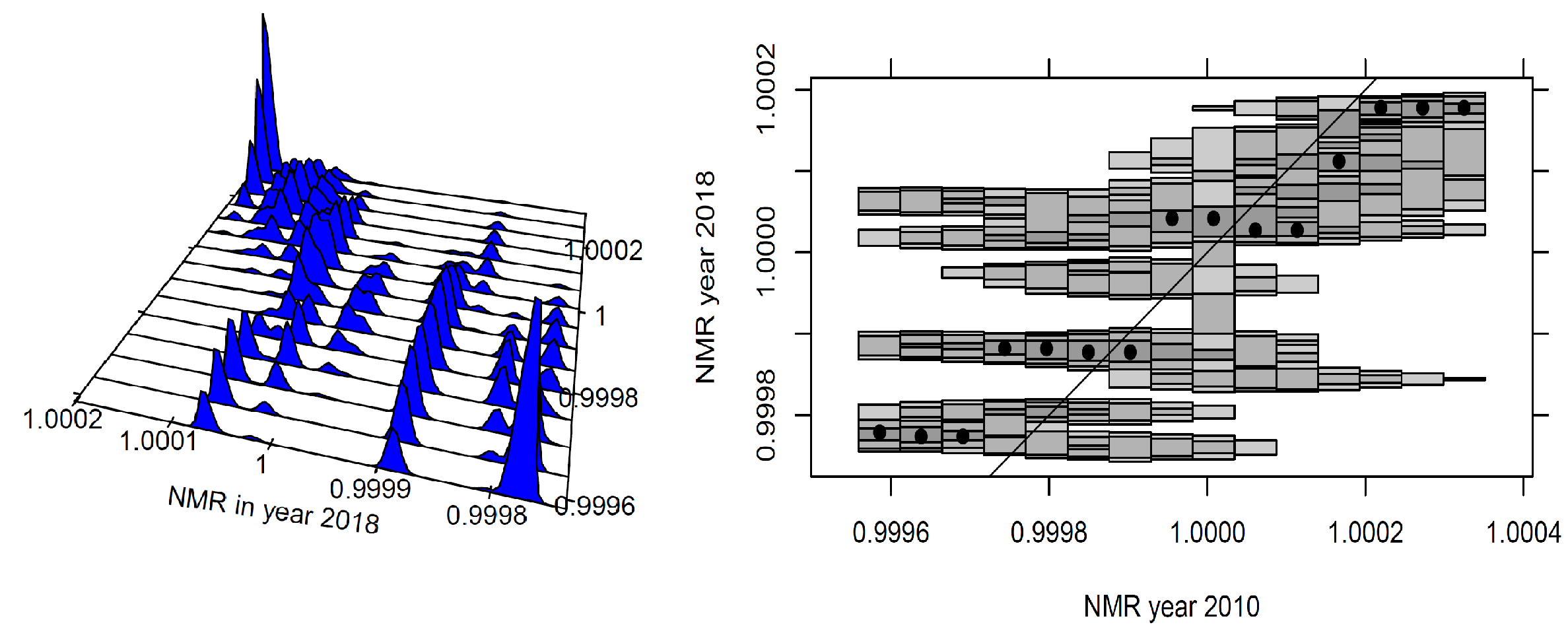
Municipal level: 2+? convergence clusters

At the municipal level there are fewer clusters but no signs of sigma convergence

13 / 20

NPIR at both levels

State level: 2 convergence clusters

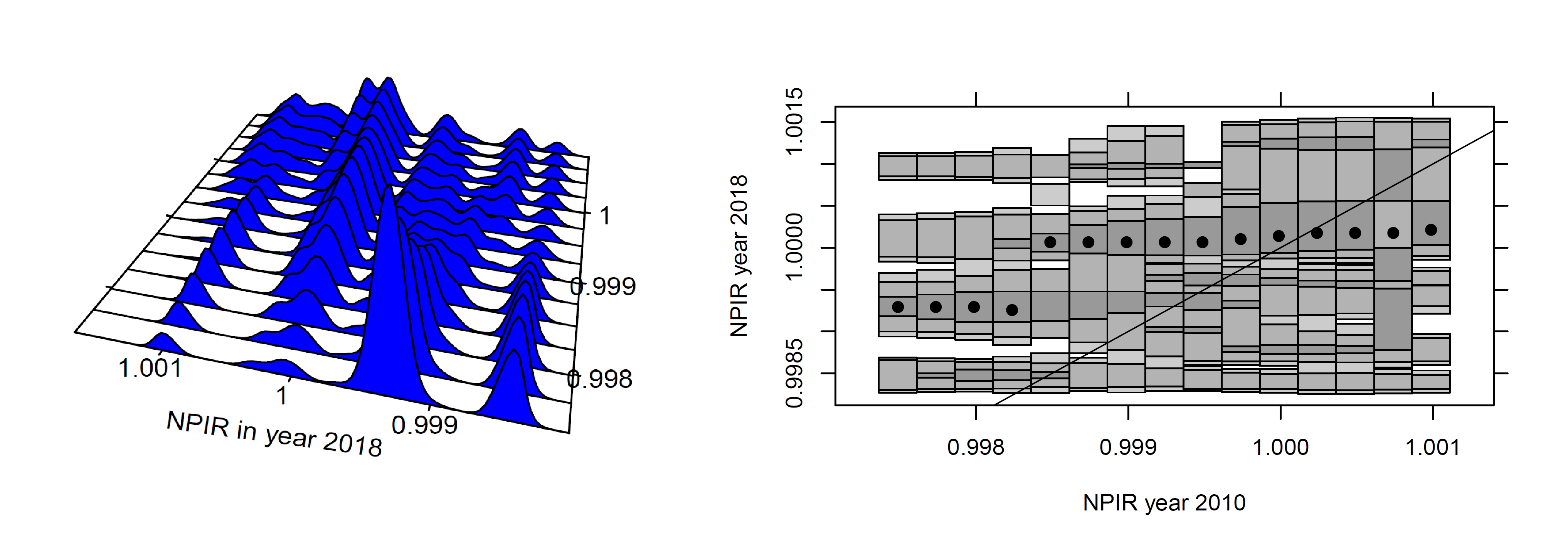
Municipal level: 2 convergence clusters and stagnation

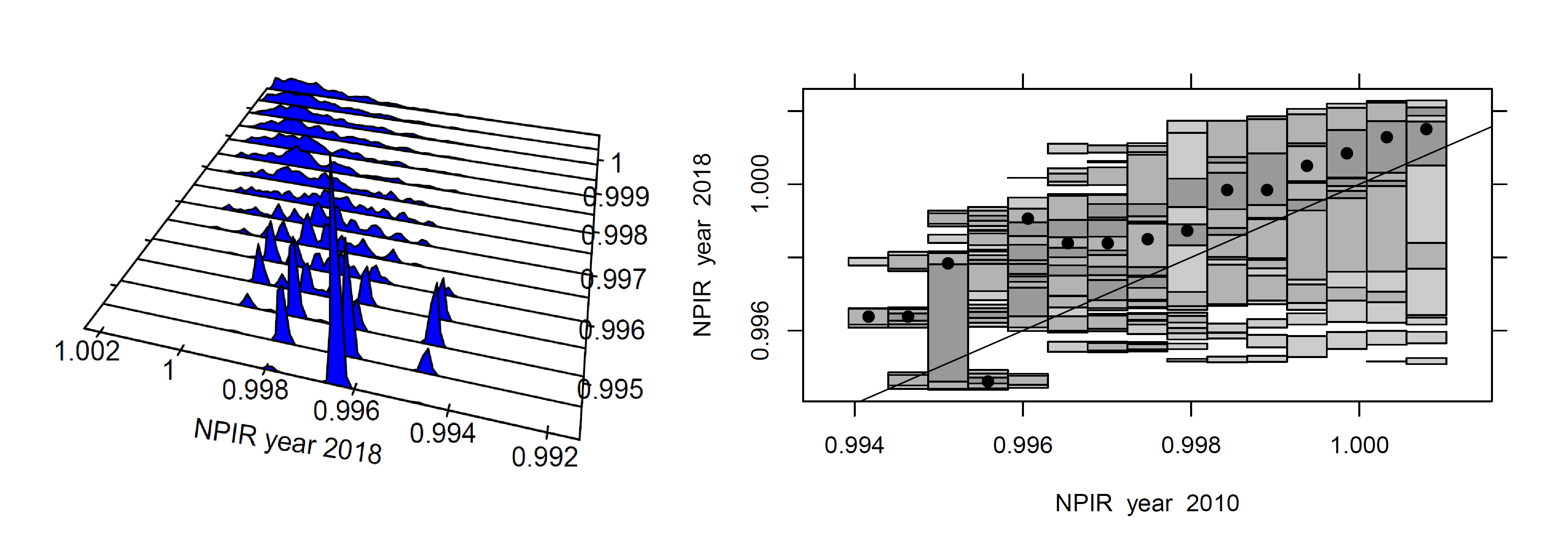
the same number of clusters but stagnation patterns are strong at the municipal level.

14 / 20

(4) Spatial Autocorrelation (Theory)

High Intuition Concept

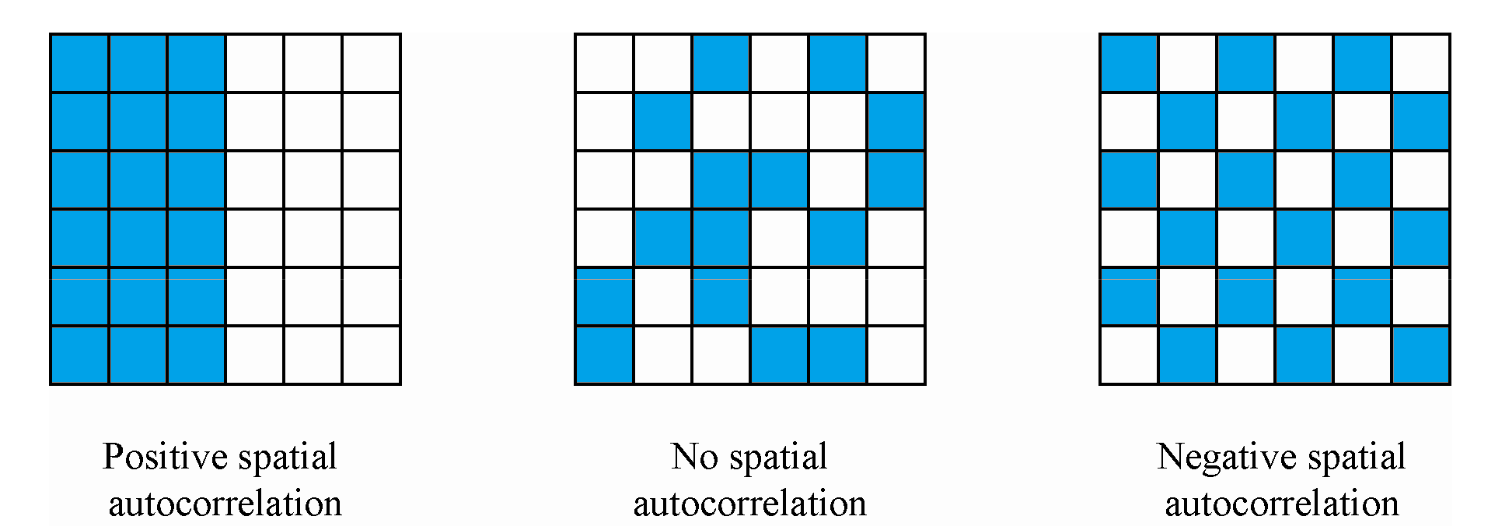
More Formal (less intuitive)

$$I = \frac{\sum_i\sum_j w_{ij} y_i.y_j}{\sum_i y_i^2} = \frac{\sum_i (y_i \times \sum_j w_{ij} y_j)}{\sum_i y_i^2}.$$

Differential Moran's I ( $y_{i,t}−y_{i,t−1}$ )

We compute the Moran's I for the variable $y_{i,t}−y_{i,t−1}$.

If there is a fixed effect $\mu_i$ related to location $i$, it is possible to present the value at each location for time $t$ as the sum of some intrinsic value and the fixed effect. $y_{i,t} = y*_{i,t} + \mu_i$

15 / 20

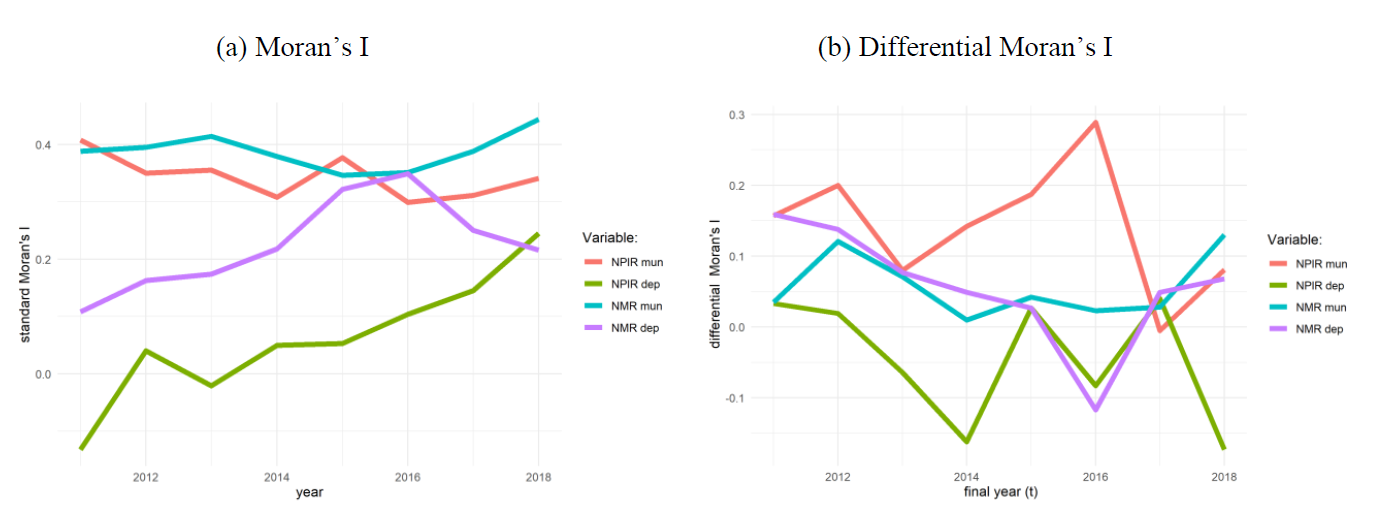
(4) Spatial autocorrelation (Results)

State level: Moran's I statistic is significant, differential Moran's I is not significant (not robust)
Municipal level: Standard and Differential Moran's I significant (robust)
Space matters at the Municipal level

16 / 20

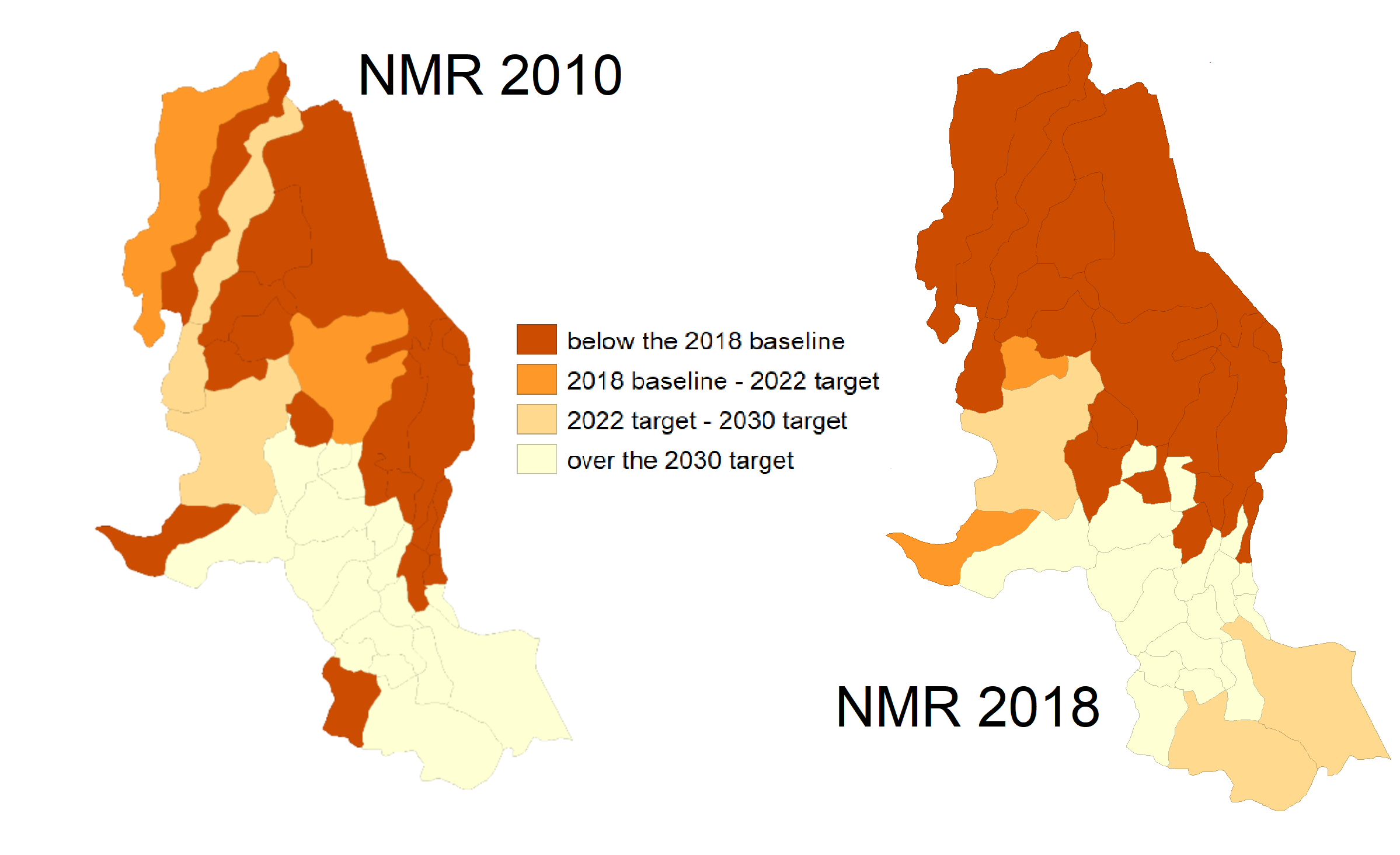
(5) Policy discussion

Vertical and horizontal policy coordination, spillovers and borders.
Spatial spillovers from neighbors can have both positive and negative effects on the convergence path of a region.
It could be more appropriate for the formulation of national development plans to have targets at the state level

17 / 20

(5) Concluding Remarks

Uplifting results "on average" :

The dispersion of non-crime (crime) rates at the state level has decreased. On average less homicides but more personal injuries.
Global convergence on average at the state level, while fast beta convergence at the municipality level.

Beyond classical convergence :

Regional differences matter in both disaggregation levels.
Multiple local convergence clubs; with more clubs at the state level.

The Role of Space

Subsequent Differential Moran's I are robust and significant at the municipality level only
Results at the state level for NMR are not conclusive and similar to the ones reported by Royuela et al 2015.

18 / 20

(5) Concluding Remarks

Implications and further research

Convergence clusters help us to find regions with similar outcomes, coordination among them can be promoted.
Strong spatial autocorrelation suggest the possibility of applying spatial filters in order to remove the spatial component of crime variables.
At the state level (including more variables) a probit model may help us to find the determinants for a conditional "jump" to the upper clusters.
As many municipalities have small population, crime rates have high variance instability. Empirical Bayes methods can be used.

19 / 20

Thank you very much for your attention

You can find the working paper on my website https://felipe-santos.rbind.io

If you are interested in our research please check our QuaRCS lab website
https://quarcs-lab.rbind.io/

Quantitative Regional and Computational Science Lab

20 / 20

Motivation:

Beyond GDP, socio-economic variables and their convergence are relevant for development studies (Royuela et al 2015)

Persistent income differences, differences in health indicators and in "general" regional inequality in Colombia.

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

Regional Convergence, Spatial Scale, and Spatial Dependence:

Evidence from Homicides and Personal Injuries in Colombia 2010-2018

Felipe Santos-Marquez Master’s studentGraduate School of International DevelopmentNagoya University, JAPAN Carlos Mendez Graduate School of International DevelopmentNagoya University, JAPAN

Prepared for the 2020 Bolivian Conference on Development Economics July 27th [ Working paper available at: https://felipe-santos.rbind.io/]

Motivation:

Research Objective:

Methods:

Main Results:

Outline of this presentation

(1) Data:

Non-crime variables over time

(2) Global convergence:

Classical Convergence results (NMR)

States- Sigma and Beta convergence

Municipalities - ONLY Beta convergence

Beta and sigma convergence summary

(3) State and Municipality disaggregation:

The distribution dynamics framework

The distribution dynamics framework

Convergence, divergence and stagnation

(3) Local convergence clusters

NMR at both levels

At the municipal level there are fewer clusters but no signs of sigma convergence

NPIR at both levels

the same number of clusters but stagnation patterns are strong at the municipal level.

(4) Spatial Autocorrelation (Theory)

High Intuition Concept

More Formal (less intuitive)

Differential Moran's I ( \(y_{i,t}−y_{i,t−1}\) )

(4) Spatial autocorrelation (Results)

(5) Policy discussion

(5) Concluding Remarks

Uplifting results "on average" :

Beyond classical convergence :

The Role of Space

(5) Concluding Remarks

Implications and further research

Thank you very much for your attention

Motivation:

Research Objective:

Methods:

Help

Felipe Santos-Marquez
Master’s student
Graduate School of International Development
Nagoya University, JAPAN

Carlos Mendez
Graduate School of International Development
Nagoya University, JAPAN

Prepared for the 2020 Bolivian Conference on Development Economics July 27th

[ Working paper available at: https://felipe-santos.rbind.io/]